

However, there was no mistake or contradiction by Engel & Reid in making that statement, because in the sentence immediately prior they make it clear they are discussing changes done at constant V or constant p. The following statement is not generally true:įor instance, in a closed system $\Delta U = q + w$ so what is independent of path isn't $q$, it's the sum of $q + w$. I'll address part of your confusion here: So here is a more detailed explanation of the fundamentals as well as a cookbook (foolproof) recipe for determining the change in entropy of the system and surroundings for any arbitrary irreversible process on a closed system (including worked examples of the methodology): I know that this might all sound a little confusing. So, the change in entropy of the surroundings in the irreversible process was 12.47 J/K. So, for its alternative reversible path, to achieve this same internal energy change at 300 K, the amount of reversible heat it would have to absorb would be the same 3.741 kJ. In the case of the surroundings, during the irreversible process, its internal energy increased by 3.741 kJ at the constant temperature of 300 K. This is the entropy change for the system both for the reversible path you devised as well as for the actual irreversible path. You did that correctly for the system, and determined its correct entropy change (-7.62 J/K). You must separate the system from the surroundings, and then devise an alternative reversible path for each of them separately that takes each from its initial state to its final state. From this point on, you must totally forget about the irreversible path and, instead, focus exclusively on the initial and final end states.

For the irreversible path, you correctly calculated the final state using the first law of thermodynamics.
#Entropy vs enthalpy how to
You are confused about how to calculate the entropy change for a system and surroundings that have experienced an irreversible process. San Francisco: Pearson Benjamin Cummings, 2006. Also, I fail to understand why the change in entropy for the surroundings are not equal for the two process for which the final and initial states are equal -> change in entropy is a state function and should be the same regardless of path.Įngel, Thomas, and Philip Reid. However, I don't understand why the entropy's from the two calculations are not equal. It seems that the book used the actual heat for the irreversible process. K during the process.Ĭalculation of change in entropy for reversible path:
Because the water bath thermal reservoir in the surroundings is very large, T remains essentially constant at 300. K is reversibly and isothermally compressed from a volume of 25.0 L to a volume of 10.0 L. irreversible process, which contradicts what the textbook previously stated.
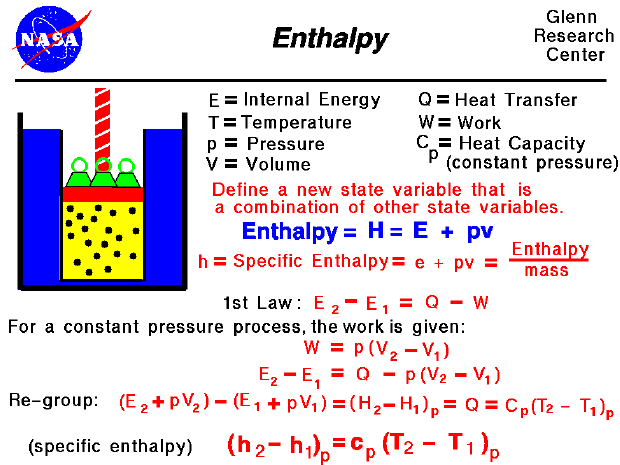
However, when the book proceeds to evaluating the change in entropy for the surroundings for a reversible vs irreersible process, the q used for evaluating the change in entropy of surroundings are not equal for the reversible v.s. irreversible processes.īecause H and U are state functions, the amount of heat entering the surroundings is independent of the path q is the same whether the transfer occurs reversibly or irreversibly. Thus, the entropy change of the surroundings which equals the quotient of the heat and temperature are equal for reversible v.s. Since the change in internal energy and enthalpy, which are equal to the heats for a constant-volume and constant-pressure process, respectively, are state functions, the heats for a reversible v.s.


 0 kommentar(er)
0 kommentar(er)
